牟合方盖是如何计算球体体积的?(如何制作牟合方盖)

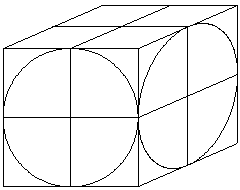
牟合方盖是什么？我相信很多人对此并不熟悉。牟合方盖是中国古代数学家刘辉发现的一种计算球体体积的方法。他希望用牟合方盖来证明九章算术的公式是错误的，但最终没有实现，但牟合方盖的发现具有重要的历史意义，牟合方盖是如何计算球体体积的？

什么是牟合方盖？

牟合方盖是中国古代数学家刘辉首先发现并采用的一种计算球体积的方法，类似于现在的微元法。因为它使用的模型就像牟合的方形盒子，所以被称为牟合方盖。

牟合方盖指的是什么？

牟合方盖是两个圆柱体的公共部分，当一个正立方体用圆规从纵横两侧切割圆柱体时。刘辉在他的注中对牟合方盖有以下描述：取八块立方棋，均使立方一寸，积之为立方二寸。规则为圆，径2寸，高2寸。又复横规之，其形状就像牟合方盖。八棋像阳马，圆然也。方率也按合盖者。即圆率也在丸中。事实上，刘辉也希望通过构建一个三维图形，每个横截面都是方形的，并将与球体在同一高度的圆形横截面相连，这个图形是牟方盖，因为刘辉只知道一个圆及其外方形的面积比π：4.他希望用牟合方盖来证明九章算术的公式是错误的。

当然，他也希望从这方面开始寻找球体积的正确公式，因为他知道牟合方盖的体积与内接球体积的比例是4:3。只要有办法找出牟合方盖的体积，可惜刘辉一直解决不了。他只能指出，解决办法是通过计算国际象棋的体积。然而，由于国际象棋的复杂形状，他没有成功。他别无选择，只能留住有能力的人来寻求解决方案：看立方米，除了封面，虽然衰杀是渐进的，但有多少是不隐藏的。判合总结，方圆相缠，浓纤诡互，不等正。判合总结，方圆相缠，浓纤诡互，不能等正。欲卑微措意，怕失正理。敢不阙疑，以为能言者。”

牟合方盖的体积计算方法：

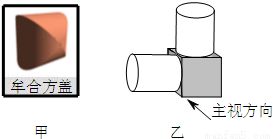
上图右边是一个正方体挖两个四棱锥(这两个四棱锥分别以上下底面为底面，以正方体中心为顶点)，正方体边长为2。r。将牟合方盖和右图几何体与平行于底面的平面同时截断，截面如上图所示。左图的截面是一个正方形，设中心到截面的距离为h，可以看出，正方形的边长是2√r2-h因此，左图的截面积为4（r2-h2）

右边的截面像一个方形环，面积是大正方形，减去小正方形的面积，边长为2r，因此，大正方形面积为4r2.从中心到截面的距离也是如此h，可以看出，小正方形的边长是2h，因此，小方形的面积是4h2.截面积为4r2-4h2。

从上面可以看出，两个几何体在同一水平位置的截面积是相等的。根据祖先的原理，它们的体积是相等的。右图的体积等于正方体的体积，减去了两个四棱锥的体积。根据锥体的体积公式，两个锥体的体积之和是正方体体积的1/3，因此几何体的体积是正方体积的2/3，即牟合方盖的体积是正方体积的2/3。r所以最后，牟合方盖体积为16r3/3。

牟合方盖的历史意义：

牟合方盖的提出充分体现了古人丰富的想象力和建立解决问题模型的智慧。刘辉是一个1700多年前的人。他以几千年前的社会知识水平思考这个问题是惊人的。这种智慧的光芒震撼了古今，闪耀着世界。他们对数学或哲学问题的执着思考和纯粹的探索精神是现代人所缺乏的，也是当前教育的一个重要方面。