对黎曼假定的了解

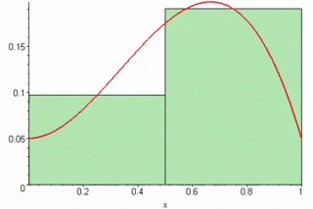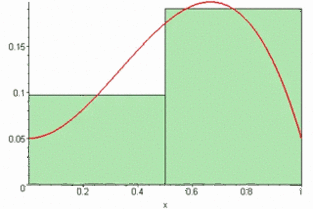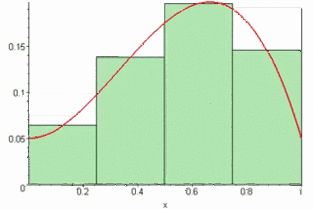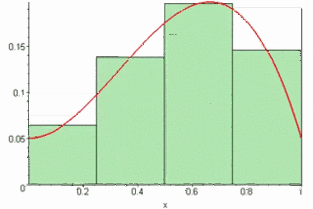
1. 质数漫衍模式24·10^n/90·10^n.

2. 用二次互反律反判，判否，即肯定是合数。用黎曼截塔函数即倒割函数剔除合数。

3. 实数1/2和虚数1/2及平方剩余的1/2的意义。待判不克不及被3,5整除的奇数P，(P－1)/2=X。X^2/P，P的整倍数又是分子的1/4。平方剩余是P的1/4(0.25/p),或3/4(0.75/p)。x取值的平方剩余有与(0.25,0.75)同余的作判否暗号，再编辑统计加总函数即可。0.25，0.75两数当作零位，分子以减一加二再求和。如77，(77－1)/2=38，38^2=58+18·77，17^2=58+3·77，38－17=11是77的约数。再有一种鉴别法是:58+2+4=64，64是平方剩余的平方数，整倍数>零倍，与零倍的64为同余，即77合数。38－2=36，

(36－8)(36+8)=36^2－64

(36－8)(36+8)=28·44=16·7·11。

另有许多简化大数的算法，略。倍数加2律。

4. 方程(略)。重要由哥得巴赫料想的双合数1+1及奇质数料想的开导而得。"1"+"1"=奇数=质数+2x^2。

5. 质数个数占天然数的比30位左右小于1%。无穷淘汰某一缓降率值，待进一步推研求判。