实空体系设想（除尘空间的电场漫衍）

4.3.2除尘空间的电场漫衍

在比电晕肇始电压Vo(V)更低的电压V(V)下,间隔阴极轴线50 x(m)处的电场强度E(V/m),可由拉普拉斯方程pE=0求得:

式中,R为集尘电极半径,m;r为阴极半径,m。

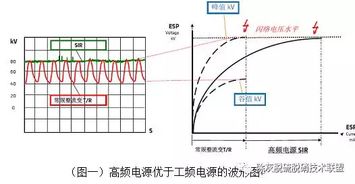
如图2-90曲线A所示,图中s为1m3的气体中浮游的粉尘外貌积总和,其巨细对应于x值根据双曲线改变。当升高电压V开始孕育发生电晕放电时,电场因离子空间电荷的作用而变形,通过解泊松方程可求得其场强值。此时的电场漫衍如图2-90曲线B所示,即因为离子空间电荷效应,使距阴极x处的电场强度比A曲线更大,因而使 电场漫衍匀称化。这种作用在放电电流强度i越大,或离子迁徙率K越小时越明显。当x格外大时,其周边电场强度E(V/m)及电流强度i(A/m)为:

式中,Vo为电晕肇始电压,

为电晕肇始电场强度,V/m;C为集成空间常数;K为离子迁徙率。

如许,除尘空间的电场漫衍,电压电流特性都受到离子迁徙率K的影响。图2-90中的曲线C所示的是与离子比力,粉尘的迁徙率非常小,因而形成了显着的空间电荷,这不但使电场的漫衍大大匀称并且使四周的电场升高,效果使火花电压低落。