量子盘算正在紧张金融产物订价题目的使用演示

FUTURE | 远见 唐豪 文

量子盘算在很多范畴都具有落地应用的充实远景，此中金融业涉及种种数值阐发使命，必要大量的量化阐发事情，通过量子盘算进步盘算速率和精度，将带来可观的社会代价。近期arXiv预印本上一个新事情（Quantum Computation for Pricing Collateral Debt Obligations），通过量子盘算要领实现一种紧张的布局性金融产物（CDO）订价，编者联络原作，在本文对该事情和其展示的量子金融应用远景举行先容。

金融阐发是将来量子盘算的一个紧张应用范畴，而且在比年来连续显现相干研究。金融业涉及到种种数值和阐发使命，比方衍生产物订价，名誉评级，外汇算法生意业务，投资组合优化等，都必要大量的定量阐发事情，而其进步的盘算速率和精度将带来庞大的社会代价。而这正是量子盘算的目的。十几年前时，量子物理学家试着运用量子力学方程式革新金融模子，比方利用薛定谔方程和费曼路径积分法来求解利率衍生产物的随机微分方程，而且将海森堡不确定性道理用于解说股价颠簸。比年来的研究则是是把量子盘算作为一个使用量子上风实现的更快的盘算东西，在量子电路中实现种种加快算法，比方量子幅度估量（QAE），量子主身分阐发（PCA），量子天生反抗网络（QGAN），量子经典混淆变重量子本收罗解器（VQE）算法，量子类似优化算法（QAOA）等算法不停涌现，并已有部门应用于金融阐发使命。

在量化金融的全部范畴中，蒙特卡罗（Monte Carlo）模仿始终发挥偏重要作用，由于只有少数金融衍生产物的随机微分方程具有剖析解，而大多数只能通过在不确定性漫衍（比方正态或对数正态漫衍）中重复多次随机设置来数值求解，是以金融产物订价会泯灭时间。量子幅度估量（QAE）算法于2002年提出，在2018年被指出可以有用取代蒙特卡罗要领，应用于金融阐发并实现平方加快，现在已在期权订价和名誉危险阐发中实现开端应用演示。

图一：金融产物分类表示图

思量到蒙特卡罗模仿的遍及性和订价模子的多样性，量子技能在金融范畴的参与仍处于起步阶段。如图一所示，金融产物重要包罗股票（Equity）、牢固收益（Fixed Income, 又称为债券Bonds）以及衍生品（Derivatives）三类。此中衍生品包罗期权（Options）、期货（Future）、交换（Swap）等多种东西，以及资产包管证券（Asset-based security，ABS）等更庞大的布局性产物。衍生品既可以基于股票（Equity Derivative），也可以基于牢固收益（Fixed Income Derivative)，此中后者越发遍及。种种金融产物为金融工程提供了富厚多样的量化东西。

抵押债务凭据（Collateral Debt Obligations，或Collateralized Debt Obligations，简称CDO）便是资产包管证券ABS的一种，是紧张的布局性金融衍生产物。CDO可以看成基于牢固收益的衍生品，由于它的资产池包罗种种债务东西，按名誉评级从高到低可包罗长中短期国度债券（Sovereign Bond）、公司债券（Corporate Bonds），高收益新兴市场（Emerging Market）公司债券等等。在如许的资产池投资组合里，每个资产都有各自的违约概率，而且相互之间存在违约的相干性。CDO则是将该投资组合通常打包分为三个CDO批次（CDO Tranche），如图二所示，包罗股票批次（固然名字叫股票，实在通常由名誉评级低、乃至没有名誉评级的债券构成），夹层批次（通常由A或A +级证券构成）和高级批次（通常由名誉评级最高的AAA级债券构成）。当池中任何资产产生违约时，CDO划定由股票批次投资者起首负担丧失，假如丧失大于第一个临界点（Attachment Point），则多出的部门由夹层批次投资者负担。只有当丧失大于第二个临界点时，高级批次投资者才会亏损。高级批次投资者具有最佳的危险防护，还具有担当本金和利钱付出的优先级。依据金融危险和回报的同等性，高级批次投资者得到最低利率回报，而股票批次投资者在负担最多危险的同时得到最高收益。

图二：CDO包罗股票批次（Equity Tranche），夹层批次（Mezzanine Tranche）和高级批次（Senior Tranche），各批次负担丧失的次序差别。

CDO可以有用地爱护高级批次免于丧失。CDO是一种有效的信贷东西，可以以非常定量的方法盘算和重新安排信贷危险，现在金融行业具有名誉危险治理的猛烈需求，是以CDO在量化金融中得到遍及研究并不停美满。到本事情报道之前，还从未有量子算法在CDO等庞大布局性金融东西的应用报道。

CDO订价模子

CDO的订价，指的便是盘算出每个批次大概负担丧失的盼望值，除以这个批次的资产代价，得到这个批次面对的丧失率，那么该批次该当付出投资人相称的收益率实现危险和收益的均衡。

CDO每个批次负担丧失与总丧失的干系函数雷同于期权订价中的收益函数（pay-off function）。看涨期权的代价在特定临界点后随着资产代价的提拔以1为斜率线性增进，期权代价为正（in the money）。CDO批次丧失同样在特定临界范畴内随总丧失线性增进。这种和特定临界点举行比力的操纵都可以在量子线路的比力器模块中实现，将在后文中提及。

资产池的总丧失取决于每个资产的违约情形。资产代价遵照一个不确定性漫衍随机上下浮动，当代价低于某阈值时以为该资产违约。这个不确定性漫衍模子中以高斯漫衍最常见。但实际天下中，代价漫衍每每还存在偏度和峰度。正态逆高斯（Normal Inverse Gaussian, 简称NIG）模子，则可以通过更多的参数调控，实现机动的偏度和峰度，能更好地解说高斯漫衍不克不及解说的CDO市场“相干性微笑”（Correlation Smile）等征象。如图三所示，图ab分别是用四个量子比特导入的高斯漫衍，以及切合某个真实CDO市场数据的正态逆高斯漫衍。

图三：用4个量子比特加载高斯漫衍或NIG漫衍表示图。该NIG漫衍的偏度为1，峰度为6。

CDO订价必要重点细致的，是大量资产之间违约变乱存在必然的相干性，数学上通常采纳copula模子形貌。不管单身分高斯copula， 照旧NIG copula，都可以利用Vasicek提出的条件独立要领（Conditional independence approach），将每个资产i之间的违约危险相干性转化为与体系危险Z的相干性。此时受体系危险Z 影响下的资产违约概率为：

F代表Z的漫衍函数，在本文中是高斯漫衍或NIG漫衍。公式中包罗的原始独立违约概率，可以从其汗青体现中得到；与Z的相干性参数则可以通过校准市场数据得到的相干参数。

利用这种条件独立性模子，预期总丧失则是Z取特定漫衍中差别值的各资产违约孕育发生丧失之和的盼望值。

CDO订价的量子线路结构I——加载相干联的违约危险

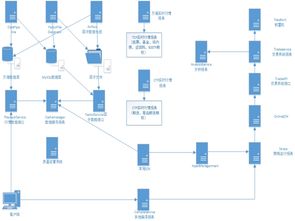
要将量子盘算应用于CDO订价，起首必要将投资组合中的资产危险以及相干性加载到量子电路中。量子线路框架如图四所示。

图四：CDO订价的量子线路框架。

（1）起首通过Lx加载违约危险互不相干的独立的资产，使|1>态的概率便是资产 i 的独立违约概率p_i。

（2）同时加载体系危险Z的高斯漫衍或NIG漫衍（图中Load Z distribution模块）。对付高斯漫衍，利用IBM Qiskit中自带的Uncertainty Model和Conditional Independence Model步伐。对付NIG漫衍，作者则上传了相应步伐，为Qiskit开源步伐库的富厚美满作了必然奉献。

（3）然后通过Lz处置惩罚资产违约危险之间的相干性，扭转使|1>态的概率变为受体系危险z影响的p_i(z)。p_i(z)与z和p_i的函数表达式上文已给出。运算符Lz的slope和offset与z和p_i干系的细致推导可参阅论文的附录II。Lz运算符利用n_z个量子比特，就可以将漫衍分离化到2 的n_z次方个槽中。比方，具有3个量子位，z的范畴在0到7之间，对应于高斯漫衍的正负三个方差区间。对付z=4=1*1+0*2+1*4-1，量子比特1和3会打开其相应的受控扭转门，而量子比特2不会。通过如许的仿射映射，z值对线性扭转的影响被编码在量子电路中。

（4）利用S进一步求和投资组合的总丧失。即系数i乘以资产i 的给定违约丧失并求和，假如资产i违约，则系数i为1，反之为0。系数i为1的概率正是Lz运算符输出的p_i(z)。

CDO订价的量子线路结构II——盘算批次丧失

图四的量子线路中另有最终一个紧张的模块，C&R，即包罗了比力器运算符C和分段线性扭转运算符R。

比力器运算符是完成金融产物订价使命的紧张构成部门。在期权订价的量子盘算中，它用于将资产代价与利用代价举行比力。这里利用比力器运算符C，对上述运算符S输出的丧失总和值和每个批次的牢固下临界点举行比力。假如丧失总和大于该批次下临界点，C将会从|0>态翻转到|1>态，不然连结|0>态稳定。

与此同时，另有一个目的量子比特，它将在比力器比特的操纵下扭转其状态。也便是说，通过比力器运算符C和分段线性扭转运算符R实现如下转换：

如许一来，目的量子比特在|1>态的概率P1则包罗了特定批次的预期丧失E [L_tranche]的信息，详细推导可参考论文。只要得到P1，就能盘算出批次丧失，除以该批次的资产代价，就得到该批次投资人作为危险赔偿应得的收益，实现CDO订价。

那么如何测得概率P1呢？我们知道对一个扭转了恣意角度的量子态举行丈量，它会坍缩到一组选定的正交基矢。丈量单一正交基矢的重量不克不及还原相位，丈量的概率值对应是模平方，已经抹除了相位信息。采纳量子态层析技能是可行的，但是必要预备多份样本，而且必要多组基矢丈量，多次丈量粉碎量子态来得到相位。

量子幅度估量（Quantum Amplitude Estimation, QAE）算法，它的内核是量子相位估量（Quantum Phase Estimation），不必要粉碎目的量子态就能有用得到其相位、盘算出P1。QAE的重要头脑便是，采纳m个帮助量子比特，则可以天生2的m次方个差别的值，就像切蛋糕一样把π分成了2的m次方份。对m个量子比特举行丈量，得到的二进制数转换成十进制数y, 占了y小块蛋糕，那么丈量的角度约即是y除以2的m次方乘以π。怎样将丈量角度映射到m个帮助量子比特中，涉及到量子反傅立叶变更等操纵，详细可以参阅论文。帮助量子比特数m决定估算的精度，普通大于3比力符合。

CDO订价的量子盘算示例

以一个示例来阐明CDO的订价。该CDO资产池包罗四个资产。如左表所示，第二、三四列分别为资产的给定违约丧失、独立违约概率以及对体系危险敏感性。右表的第二第三列表现了CDO批次的下临界点和上临界点。

对付此使命，必要n_k = 4个量子比特来表现Lx运算符中的四个资产。在Lz运算符中利用n_z = 4个量子比特孕育发生2 ^ 4 = 16个槽位用于展示体系危险Z的不确定性漫衍，即前文中的图三。利用条件独立性模子，资产违约危险之间的相干性将转换为体系危险Z的相干性。

在加权和运算符S中，思量全部资产均违约时，此投资组合的最大累计丧失为 7（小于2的3次方减1），是以利用n_s = 3个量子比特对总丧失举行编码。

量子电路利用Qiskit内置的分段线性扭转函数，此中包罗比力器C和分段线性扭转器R。内置函数利用breakpoints数组记载毗连点，并利用slopes和offsets数组记载斜率和偏移量。

图五：股票、夹层和高级批次的丧失与总丧失的干系图，每子图小框中的三个数组分别表现breakpoints、slopes和offsets数组

举行完以上设置就可以利用QAE算法估P1，然后转换求得每个批次的丧失盼望值。利用Qiskit的QASM模仿器，QAE中利用m = 4个帮助量子比特, 求得效果与经典蒙特卡洛效果举行比力。如图六表现Z为NIG漫衍时，两种要领的效果非常符合。别的当Z遵照高斯漫衍时效果也同等。假如增添帮助量子比特数m，估算的精度还可进一步进步。

图六：盘算所得股票、夹层和高级批次的丧失。蓝色柱和赤色虚线分别为量子盘算和蒙特卡罗效果

用上图所得的批次丧失除以批次资产（即批次上下临界点之差），就可以盘算出股票，夹层和高级批次的批次收益。高级批次在实际中便是低回报的，起首是由于它是蒙受亏损的危险最小，其次由于高级批次的资产代价很大，每每占总资产的80％以上。股票和夹层批次的回报率算出来偏高，实际中通常分别为15-25％、5-15％左右。一方面是这里设的独立违约概率比实际情况高，另一个缘故原由是，这里专注根本模子布局就没有思量资产的规复率。规复率通常设置为40％，这意味着当资产违约时，可以实验通过出售一些房地产等方法来规复某些代价以赔偿投资者。最大丧失将即是总名义值乘以（1-规复率）。在此示例中，40％规复率会使给定违约丧失变为1.2、1.2、0.6和1.2，而批次临界点连结稳定，就会低落批次丧失。

量子盘算应用于金融题目的商议瞻望

CDO是相对先辈和庞大的布局化金融产物，只管在2008年金融危急时期存在一些争议，但CDO仍旧在量化金融中被遍及研究并不停美满。这项事情实现了相比高斯模子更具上风的正态高斯逆模子。另有Variance Gamma等适于CDO订价的新型模子，以及期货等更多衍生品的订价模子，它们和期权、CDO一样，都可以用量子QAE算法取代蒙特卡罗要领实现。

图七：枚举更多金融量化题目及大概的量子盘算要领

除了衍生品订价题目，如上图所示，金融范畴还存在其他大量的量化阐发场景，必要办理每天都在孕育发生的海量金融数据阐发题目。随着量子呆板进修的进展，一些量子版本的回来、分类算法及量子神经网络模子将在金融时间序列相干的各项应用场景中发挥作用。别的，实用于NISQ情况的变重量子算法，以及基于伊辛机模子的量子退兵器，都可用于金融场景中遍及存在的优化题目。总之，量子算法金融题目应用的越发宽阔无垠的大概，亟待人们去探究实践。

论文第一作者为上海交通大学物理与天文学院助理研究员唐豪博士，通迅作者为唐豪博士和金贤敏传授。第一作者还对其在伦敦商学院举行牢固收益及利率衍生品量化阐发进修的讲课传授予乃至谢。

论文得到IBM Qiskit Finance部分卖力人Stefan Woerner博士的存眷，并配合商量将本事情示例在Qiskit社群的进一步分享。

论文链接：http://arxiv.org/abs/2008.041